PhastFT

PhastFT is a high-performance, "quantum-inspired" Fast Fourier Transform (FFT) library written in pure Rust.

Features

• Two FFT algorithms: Decimation-in-Frequency (DIF) and Decimation-in-Time (DIT) for different use cases
• Simple implementation using the Cooley-Tukey FFT algorithm
• Performance on par with other Rust FFT implementations
• Zero unsafe code
• Takes advantage of latest CPU features up to and including AVX-512, but performs well even without them
• Selects the fastest implementation at runtime. No need for -C target-cpu=native!
• Optional parallelization of some steps to 2 threads (with even more planned)
• Up to 5x lower memory usage than RustFFT
• Python bindings (via PyO3)

Limitations

• Only supports input with a length of 2^n (i.e., a power of 2) -- input should be padded with zeros to the next power of 2

Planned features

• Bluestein's algorithm (to handle arbitrary sized FFTs)
• More multi-threading
• More work on cache-optimal FFT

How is it so fast?

PhastFT is designed around the capabilities and limitations of modern hardware (that is, anything made in the last 10 years or so).

The two major bottlenecks in FFT are the CPU cycles and memory accesses.

We picked an efficient, general-purpose FFT algorithm. Our implementation can make use of latest CPU features such as AVX-512, but performs well even without them.

Our key insight for speeding up memory accesses is that FFT is equivalent to applying gates to all qubits in [0, n). This creates the opportunity to leverage the same memory access patterns as a high-performance quantum state simulator.

We also use the Cache-Optimal Bit Reversal Algorithm (COBRA) on large datasets and optionally run it on 2 parallel threads, accelerating it even further.

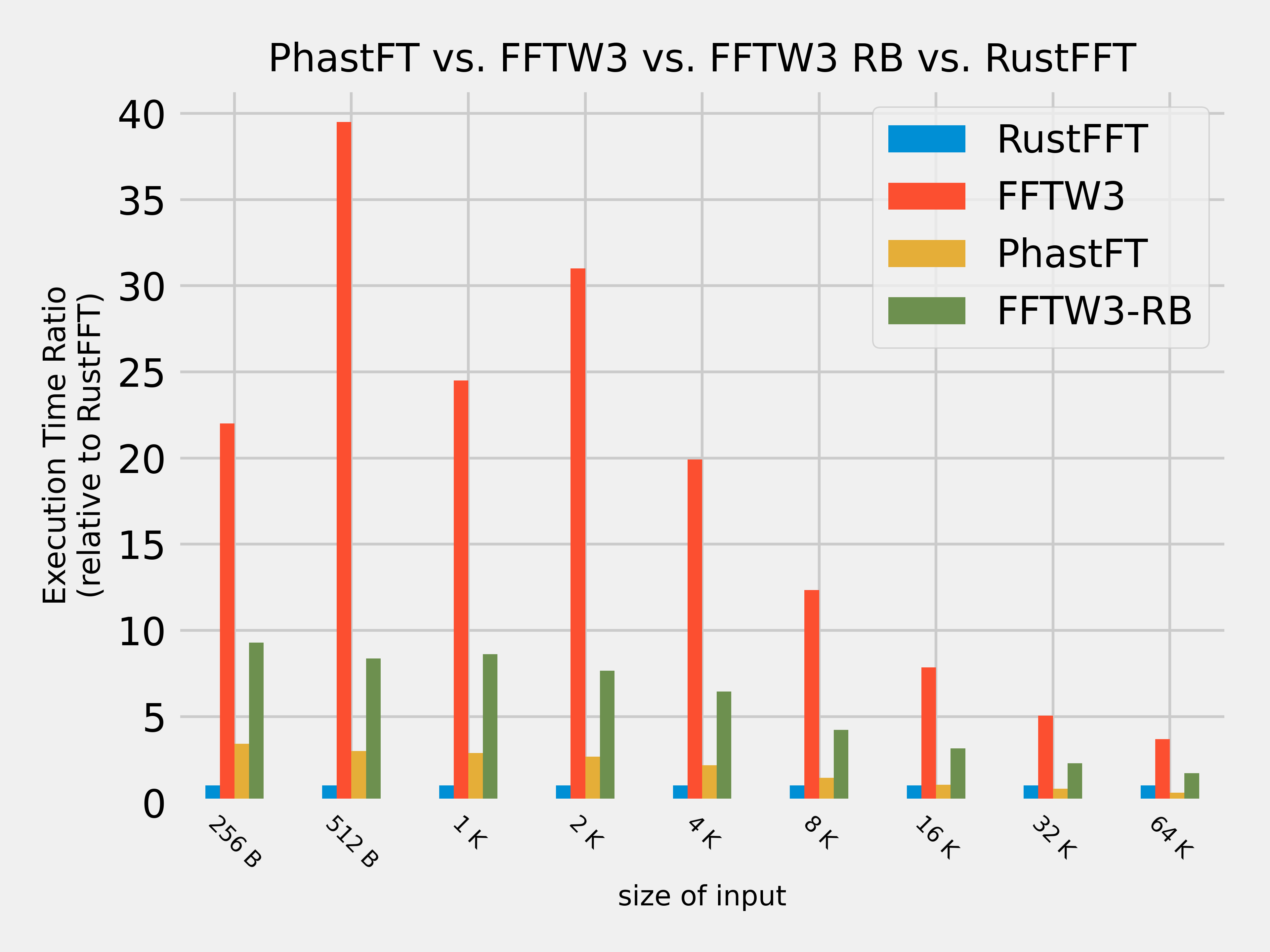
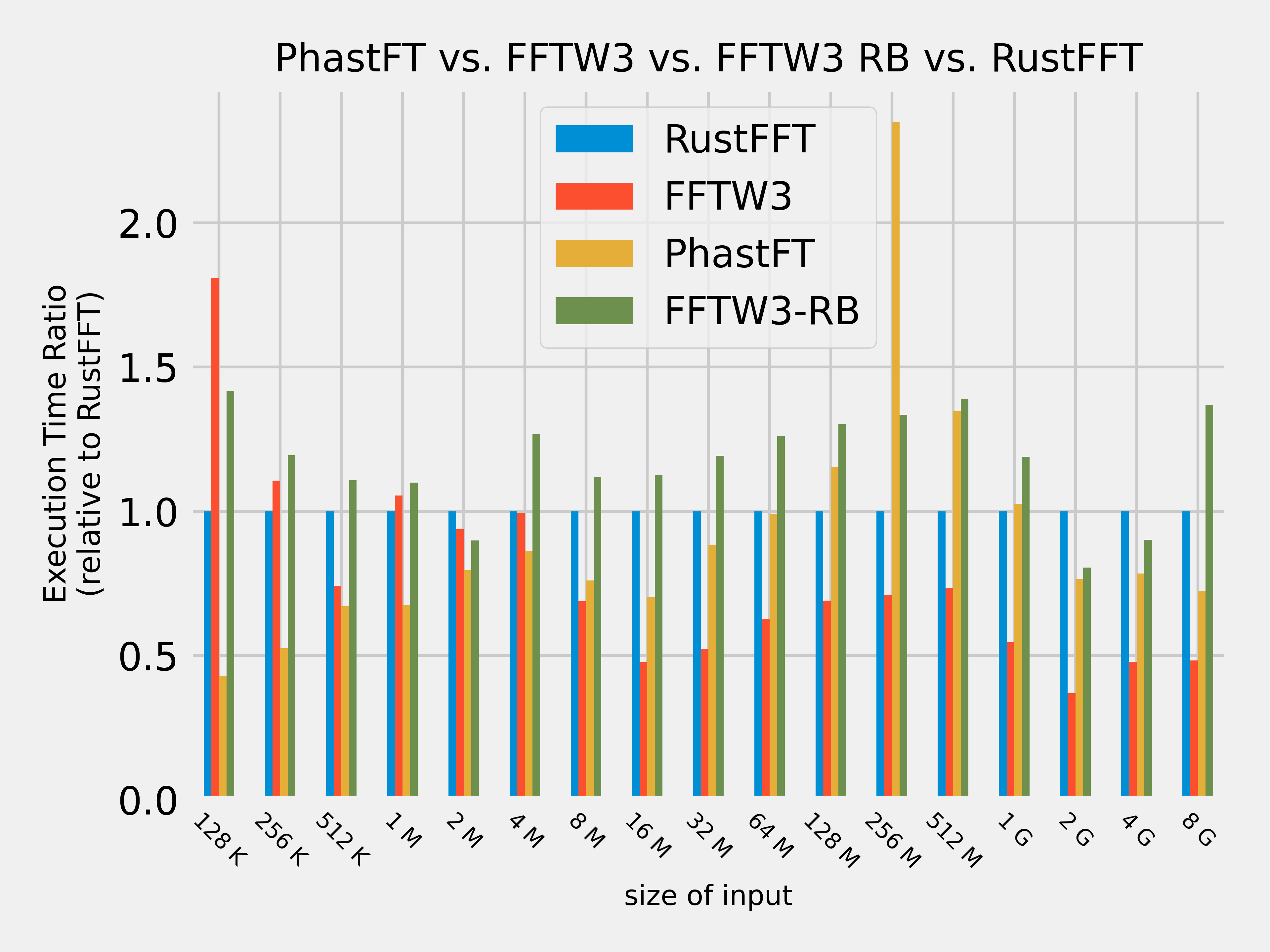
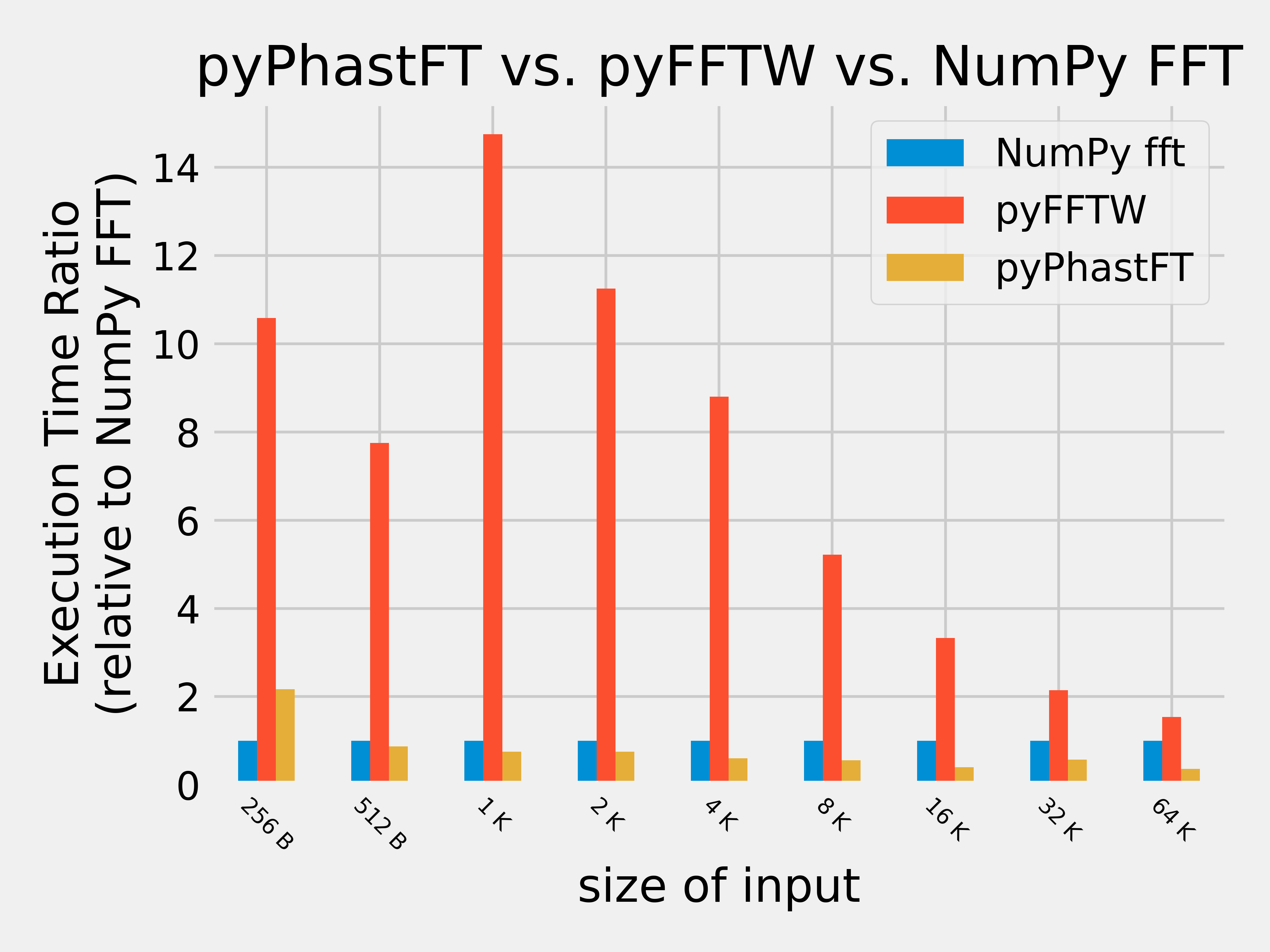
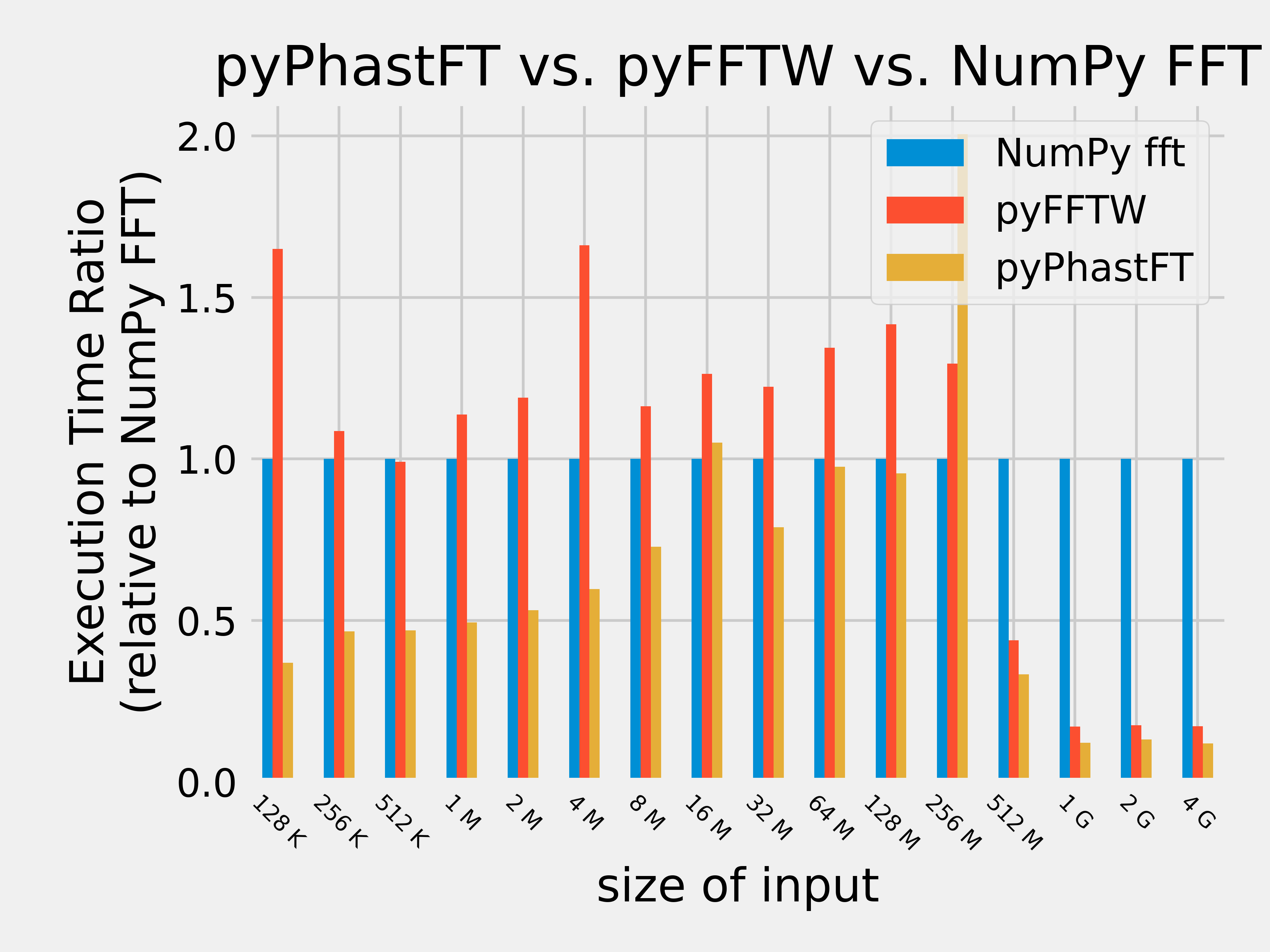
All of this combined results in a fast and efficient FFT implementation competitive with the performance of existing Rust FFT crates, including RustFFT, while using significantly less memory.

Quickstart

Rust

use phastft::{planner::Direction, fft_64};

// Using the default DIF algorithm
let big_n = 1 << 10;
let mut reals: Vec<f64> = (1..=big_n).map(|i| i as f64).collect();
let mut imags: Vec<f64> = (1..=big_n).map(|i| i as f64).collect();
fft_64(&mut reals, &mut imags, Direction::Forward);

Using DIT Algorithm

use phastft::{fft_64_dit, fft_64_dit_with_planner, planner::{Direction, PlannerDit64}};

// Using DIT algorithm - may have better cache performance for some sizes
let big_n = 1 << 20;
let mut reals: Vec<f64> = (1..=big_n).map(|i| i as f64).collect();
let mut imags: Vec<f64> = (1..=big_n).map(|i| i as f64).collect();

// Simple API
fft_64_dit(&mut reals, &mut imags, Direction::Forward);

// Or with a reusable planner for better performance with multiple FFTs
let planner = PlannerDit64::new(big_n, Direction::Forward);
fft_64_dit_with_planner(&mut reals, &mut imags, &planner);

Complex Number Support (Interleaved Format)

When the complex-nums feature is enabled, you can also use the interleaved format with the num_complex::Complex type:

use phastft::{
    planner::Direction,
    fft_64_interleaved
};
use num_complex::Complex;

let big_n = 1 << 10;
let mut signal: Vec<Complex<f64>> = (1..=big_n)
    .map(|i| Complex::new(i as f64, i as f64))
    .collect();
fft_64_interleaved(&mut signal, Direction::Forward);

Both fft_32_interleaved and fft_64_interleaved are available for f32 and f64 precision respectively.

Python

Follow the instructions at https://rustup.rs/ to install Rust.

Then you can install PhastFT itself:

pip install numpy
pip install git+https://github.com/QuState/PhastFT#subdirectory=pyphastft

import numpy as np
from pyphastft import fft

sig_re = np.asarray(sig_re, dtype=np.float64)
sig_im = np.asarray(sig_im, dtype=np.float64)

fft(a_re, a_im)

Normalization

phastft only scales the output of the inverse FFT. Namely, running IFFT(x) will scale each element by 1/N, where N is the number of data points, and IFFT(FFT(x)) == x. If your use case(s) require(s) something different, please don't hesitate to create an issue.

Bit Reversal and Output Order

PhastFT provides two FFT algorithms with different bit reversal behaviors:

DIF (Decimation-in-Frequency) - Default Algorithm

• Input: Normal order
• Output: Bit-reversed order (by default)
• Bit Reversal Control: Can be disabled using Options::dif_perform_bit_reversal = false

use phastft::{fft_64_with_opts_and_plan, options::Options, planner::{Direction, Planner64}};

let size = 1024;
let mut reals = vec![0.0f64; size];
let mut imags = vec![0.0f64; size];

// Skip bit reversal for DIF FFT
let mut opts = Options::default();
opts.dif_perform_bit_reversal = false;  // Output stays in decimated order
let planner = Planner64::new(size, Direction::Forward);
fft_64_with_opts_and_plan(&mut reals, &mut imags, &opts, &planner);

DIT (Decimation-in-Time) - Alternative Algorithm

• Input: Normal order (bit-reversed internally)
• Output: Normal order
• Bit Reversal: Always performed on input (required for correctness)

The ability to skip bit reversal in DIF is useful when:

• Chaining multiple FFT operations without intermediate processing
• You need the output in decimated order for specific algorithms
• Performance optimization when bit-reversed output is not required

phastft finishes processing input data by running a bit-reversal permutation on the processed data.

Benchmarks

PhastFT is benchmarked against several other FFT libraries. Scripts and instructions to reproduce benchmark results and plots are available here.

Contributing

Contributions to PhastFT are welcome! If you find any issues or have improvements to suggest, please open an issue or submit a pull request. Follow the contribution guidelines outlined in the CONTRIBUTING.md file.

License

PhastFT is licensed under MIT or Apache 2.0 license, at your option.

PhastFT vs. RustFFT

RustFFT is another excellent FFT implementation in pure Rust. RustFFT and PhastFT make different trade-offs.

RustFFT made the choice to work on stable Rust compiler at the cost of unsafe code, while PhastFT contains no unsafe blocks but requires a nightly build of Rust compiler to access the Portable SIMD API.

RustFFT implements multiple FFT algorithms and tries to pick the best one depending on the workload, while PhastFT has a single FFT implementation and still achieves competitive performance.

PhastFT uses up to 5x less memory than RustFFT, which is important for processing large datasets.

What's with the name?

The name, PhastFT, is derived from the implementation of the Quantum Fourier Transform (QFT). Namely, the quantum circuit implementation of QFT consists of the Phase gates and Hadamard gates. Hence, PhastFT.